When teaching how to add, a key step is to learn the number bonds of ten- all of the different ways to make ten (e.g. 8+2, 6+4),  otherwise known as “friends of ten”. 

This is such an important step, that no matter how old the child is, it should be learnt and practiced till fluent. The importance of knowing the number bonds for ten is that this knowledge can be applied to a “make 10” strategy to help add bigger numbers, numbers that might otherwise take long to calculate. 

How to Use the Make-10 Strategy

To use this strategy, decompose (split) the smaller number to add to the bigger number to make it into a multiple of ten. Whatever is left of the decomposed number is then added on. 

How to Use the Make-10 Strategy for Adding 1-digit Numbers

In the example, 8+4, the 4 would be split to take a two to add to the 8 to make a 10. The remaining 2 is added to the 10 to make 12.

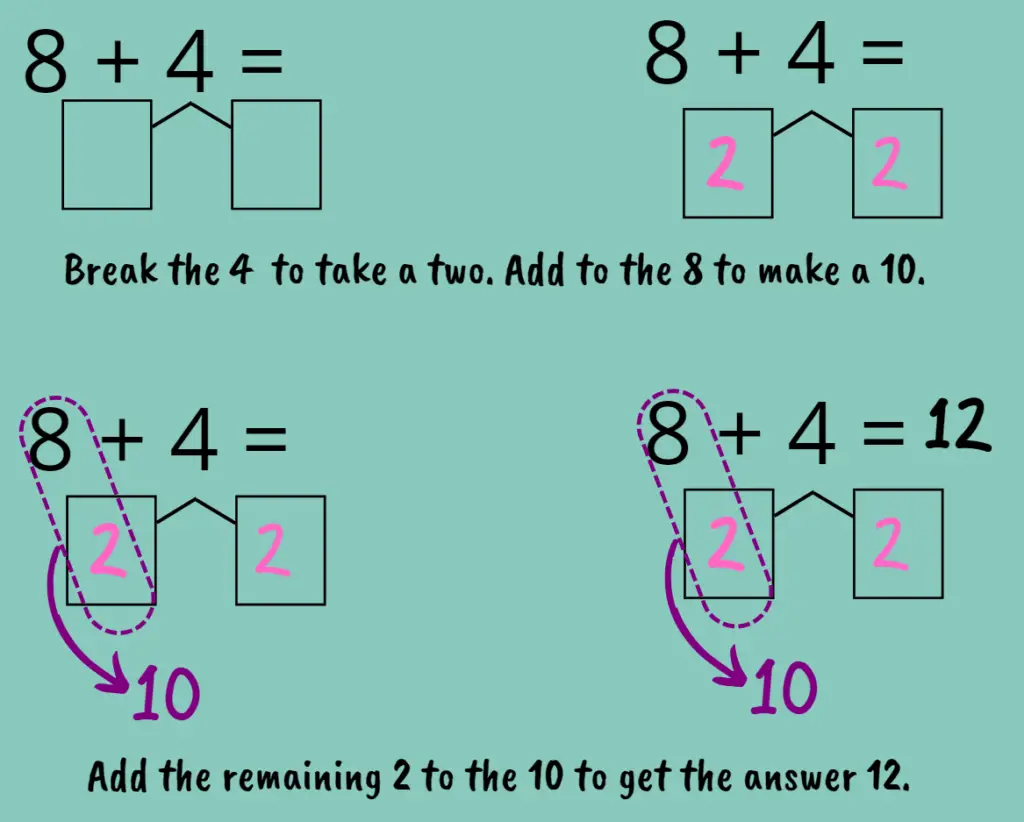
While this is a two step procedure, and it might seem like it just makes sense to count on from 8 to add 4, with practice, it greatly speeds up the process of addition, and it is a super powerful strategy to utilise when adding larger numbers- but only if fluent with the number bonds of ten, so it is vital to start implementing this strategy early on, when adding single digits. 

How to Use the Make-10 Strategy for Adding 2-digit and 1-digit Numbers

Consider the example of 37+9. Using the make 10 strategy, break the 9 and take 3 to add to the 37 to make a multiple of ten- 40. The remaining 6 is added to 40 to make 46. 

How to Use the Make-10 Strategy for Adding 2-digit and 2-digit Numbers

Now consider the example of 44 and 38. Using the make 10 strategy, break the 38 and take a 6 to add to the 44 to make 50. The remaining 32 is added to the 50 to make 82. 

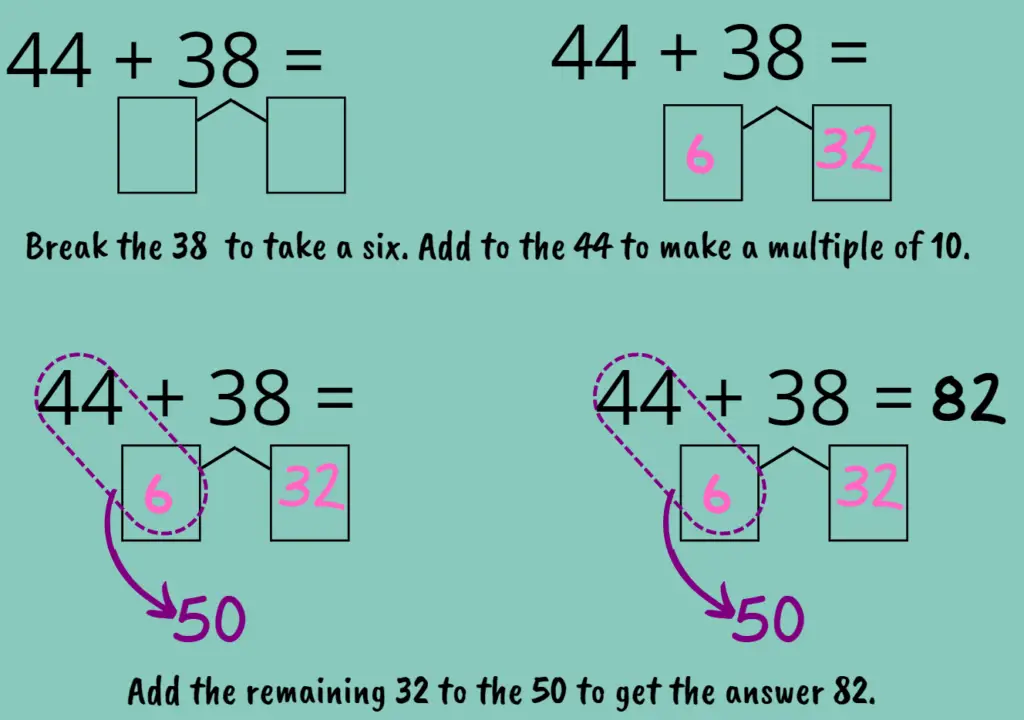
So cool right? But only after lots of practice.

It’s not an easy strategy to implement at first and as it is a two step procedure, kids might perceive it to be more work. In my experience if kids aren’t used to this method, it’s something they may resist in favour of other strategies they might already use, like counting on, using their fingers, number lines or counters. 

I’m going to be using it with my class to get their mental arithmetic more fluent and have I made two worksheets to use in my class. The worksheets have been designed where they have to use this strategy, and I can check they are implementing it correctly. 

The worksheets start with 1 digit numbers, then 2 digit and 1 digit, then finally 2 digit numbers. 

Answers included

I hope this helps some of you out!